Wolfram technologies include thousands of built-in functions and curated data on many topics.
The Wolfram Solution for Operations Research
Simulate your processes with ready-to-deploy, fully interactive models using a combination of powerful computation, analysis and dynamic report generation—all in one system, with one integrated workflow.
Underlying the Wolfram operations research solution are state-of-the-art local and global optimization techniques, sophisticated graph algorithms and efficient random number generation.
The Wolfram Edge
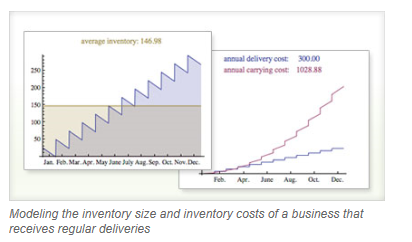
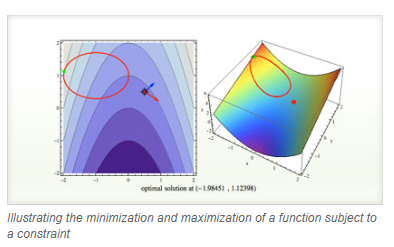
Wolfram technologies include thousands of built-in functions and curated data on many topics that let you:
- Model and optimize supply chains
- Design factory layouts for efficient flow of materials
- Solve dynamic vehicle-allocation problems
- Maximize airline revenue using leg-based and network-based seat inventory management
- Optimize maritime transport operations such as ship routing, scheduling and fleet utilization
- Perform schedule planning of aircraft and crew members and operations of aviation infrastructure such as airports and air traffic
- Develop computer simulations to minimize outpatient wait times in hospitals, explore queueing networks in material handling systems and more
- Analyze queueing systems and perform Markov process computations
- Perform effective project management using critical path analysis or PERT techniques
- Improve system reliability
- Estimate the lifetime of mechanical assemblies and biological systems
How Wolfram Compares


Does your current tool set have these advantages?
- Automatic, interactive interface construction to visualize your simulations, examine model sensitivity to parameter changes and more
Unique to Wolfram technologies
- Easy development of computer simulations of stochastic processes, discrete events and more, using built-in functions such as RandomReal, RandomInteger and RandomComplex
C/C++, Java and other programming languages require importing libraries and writing lengthy code for random number generation from continuous and discrete distributions
- Automated precision control and arbitrary-precision numerics produce highly accurate results to ill-conditioned problems
Excel, Matlab and other systems that rely on finite-precision numerics can cause serious errors due to lack of precision
- Built-in functionality for constrained and unconstrained optimization, statistical analysis and computation, curve fitting and a range of other application areas
Matlab requires the purchase of multiple toolboxes
- Easy-to-use parallel computing capabilities for solving computation- or data-intensive problems on multicore computers or grids
Extensive programming is required to parallelize processes in all other systems
- Integrated access to historic and current financial, socioeconomic, geographic and scientific data immediately suitable for computation
Unique to Wolfram technologies
- Complete workflow, from simulation to analysis to typeset documents or interactive slide shows, in a single document
Key Capabilities
Wolfram technologies include thousands of built-in functions for computation, modeling, visualization, development and deployment »
Operations research specific capabilities:
- Estimate the lifetime of mechanical assemblies and biological systems using built-in survival analysis functionality »
- Complete functionality for reliability analysis, including importance measures for pinpointing subsystems that help improve system reliability »
- Advanced graph algorithms, including Dijkstra, Kruskal, Bellman–Ford and more, for network routing applications such as internet congestion control, design of high-speed communication networks and other applications
- State-of-the-art functionality for network analysis and graph computation, including several graph metrics such as centrality measures, distance measures and more »
- Efficient random number generation for simulating events, estimating probabilities, numerically testing symbolic results and more »
- Free-form linguistic input produces immediate results without the need for syntax »
- Instantly create interactive interfaces to examine model sensitivity to parameter changes »
- Built-in functions for solving local and global optimization problems, both numeric and symbolic, including constrained nonlinear optimization »
- High-level support for mathematical model building using calculus, probability and graph theory
- Linear, nonlinear, logit, probit, generalized linear and other regression models for statistical analysis »
- Estimation of distribution parameters from data and testing of goodness of fit of data to distributions
- More statistical distributions than any other system, with the ability to define new distributions from data, formulas or other distributions »
- Built-in support for more than 4,500 units—including free-form linguistic entry, conversions and dimensional consistency checking across graphics and numeric and symbolic calculations »
- Support for a large number of random processes, including parametric processes, finite Markov processes, queueing processes, time series processes and stochastic differential equation processes.
- Support for discrete-time and continuous-time finite Markov processes and for finite and infinite queues and queueing networks with general arrival and service time distributions
- Solve linear programming problems using simplex, revised simplex or interior point methods
- Multidimensional optimization problem solving using automated algorithm selection or user-specified methods such as simulated annealing, Nelder–Mead, differential evolution and random search »
- Built-in support for parallel processing and GPU computation with CUDA or OpenCL for high-speed, memory-efficient execution
- Generate dynamic reports containing graphics, text and interactive applications »
- Instantly deploy your interactive models using Wolfram Player or webMathematica



